Multiplication of a Decimal by 10, 100, 1000

The working rule of multiplication of a decimal by 10, 100,
1000, etc… are:

When the multiplier is 10, 100 or 1000, we move the decimal
point to the right by as many places as number of zeroes after 1 in the
multiplier.

Rules for Multiplying Decimals by 10 100 and 1000

To Multiply a decimal number by 10, 100 and 1000, we simply shift the decimal point to the right by one, two and three places respectively. If there are no sufficient digits for shifting the point to the right, we add zeros to the extreme right.

Let us consider some examples.

1. To multiply a decimal by 10, move the decimal point in
the multiplicant by one place to the right.

For examples:

(i) 834.7 × 10

Here we multiplied the number 834.7 by 10 so we move 1 place to the right.

Or,

    834.7 × 10

= (8347/10) × 10

= 8347/1

= 8347

(ii) 73.5 × 10 = 735

(iii) 100.9 × 10 = 1009

2. To multiply a decimal by 100, move the decimal point in
the multiplicand by two places to the right.

For examples:

(i) 98.26 × 100

Here we multiplied the number 98.26 by 100 so we move 2 places to the right.

Or,

98.26 × 100

= (9826/100) × 100

= 9826/1

= 9826

(ii) 6.006 × 100 = 600.6

(iii) 0.77 × 100 = 77

3. To multiply a decimal by 1000, move the decimal point in the
multiplicand by three places to the right.

For examples:

(i) 793.41 × 1000

Here we multiplied the number 793.41by 1000 so we move 3 places to the right.

Or,

793.41 × 1000

= (79341/100) × 1000

= 79341 × 10

= 793410

(ii) 9.15 × 1000 = 9150

(iii) 0.017 × 1000 = 17

4. To multiply a decimal by 10, 100, 1000, etc. move the decimal point of the multiplicand as many places to the right as there are zeroes in the multiplier.

For examples:

(i) 1854.347 × 10

Here we multiplied the number by 10 so we move 1 place to the right.

(ii) 72.4 × 100

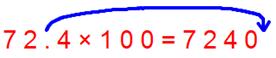
Here there is only one place after the decimal and 100 has two zeros, so we put one zero at the end of the number.

(iii) 887.43 × 1000

Only 2 places are there after the decimal, but 1000 has 3 zeros, so we put one zero at the end of the number.

5. Multiply the same decimal number by 10, 100 and 1000:

(i) 3.375 × 10

(ii) 3.375 × 100

(iii) 3.375 × 1000

Solution:

(i) 3.375 × 10 = 33.75 (Decimal point shifted to one place to the right as the multiplier has one zero to its right.)

(ii) 3.375 × 100 = 337.5 (Decimal point shifted to two places to the right as the multiplier has two zeros to its right.)

(iii) 3.375 × 1000 = 3375 (Decimal point shifted to three places to the right as the multiplier has three zeros to its right. Since there is no digit after that place, we need not place decimal point.)

Note: Remember that in multiplication of a decimal by 10, 100, 1000, etc. the decimal will be moved to the right by as many places as the number of zeroes in the multiplier and when the number of zeros is more than the digits after the decimal number, then extra zeros must be added to the product.

Worksheet on Multiplication of a Decimal by 10, 100, 1000

1. Find the product by shifting the point.

(i) 3.45 × 10

(ii) 15.89 × 100

(iii) 127.8 × 1000

(iv) 231.56 × 100

(v) 124.21 × 10

(vi) 543.9 × 1000

(vii) 285.93 × 100

(viii) 562.8 × 1000

(ix) 9.635 × 10

(x) 172.381 × 1000

(xi) 42.381 × 100

(xii) 432.09 × 10

(xiii) 72.439 × 10

(xiv) 54.368 × 100

(v) 150.38 × 1000

Answer:

1. (i) 34.5

(ii) 1589

(iii) 127800

(iv) 23156

(v) 12421

(vi) 543900

(vii) 28593

(viii) 562800

(ix) 96.35

(x) 172381

(xi) 4238.1

(xii) 4320.9

(xiii) 724.39

(xiv) 5436.8

(v) 150380

● Decimal.

5th Grade Numbers Page

5th Grade Math Problems

From Multiplication of Decimal Numbers to HOME PAGE