Converting Decimals to Fractions | Solved Examples

In converting decimals to fractions, we know that a decimal can always be converted into a fraction by using the following steps:

Step I: Obtain the decimal.

Step II: Remove the decimal points from the given decimal and take as numerator.

Step III: At the same time write in the denominator, as many zero or zeros to the right of 1(one) (For example 10, 100 or 1000 etc.) as there are number of digit or digits in the decimal part. And then simplify it.

We can express a decimal number as a fraction by keeping the given number as the numerator without a decimal point and writing 1 in the denominator followed by as many zeroes on the right as the number of decimal places in the given decimal number has.

For example:                                                                           

(i) 124.6 = \(\frac{1246}{10}\)

(ii) 12.46 = \(\frac{1246}{100}\)

(iii) 1.246 = \(\frac{1246}{1000}\)

The problem will help us to understand how to convert decimal into fraction.

In 0.7 we will change the decimal to
fraction.

First we will write the decimal
without the decimal point as the numerator.

Now in the denominator, write 1
followed by one zeros as there are 1 digit in the decimal part of the decimal
number.

= \(\frac{7}{10}\)

Therefore, we observe that 0.7 (decimal) is converted to \(\frac{7}{10}\) (fraction).

Working Rules for Conversion of a Decimal Into a Fraction:

To convert a decimal into fraction, we follow the following steps
Working Rules

Step I: Write the given number without decimal point as the numerator of the fraction.

Step II: Write 1 in the denominator followed by as many zeros as the number of decimal places in the given number.

Step III: Reduce the fraction into the lowest terms and if required change into mixed numeral.

Solved Examples on Converting Decimals to Fractions

1. Convert 6.75 into a fraction.

Solution:

Numerator of fraction = 675

Denominator of fraction = 100 (Because decimal places are 2, therefore, put 2 zeros after 1.)

So, 6.75 = \(\frac{625}{100}\)

             = \(\frac{625 ÷ 25}{100 ÷ 25}\)

             = \(\frac{27}{4}\)

             = 6\(\frac{3}{4}\)

2. Convert 924.275 into a fraction.

Solution:

Numerator of fraction = 924275

Denomination of fraction = 1000 (Because decimal places are 3, therefore, put 3 zeros after 1.)

Now, 924.275 = \(\frac{924275}{1000}\)

                     = \(\frac{924275 ÷ 25}{1000 ÷ 25}\)

                     = \(\frac{36971}{40}\)

                     = 924\(\frac{11}{40}\)

Worked-out Examples on Converting Decimals to Fractions:

1. Convert each of the following into fractions.

(i) 3.91

Solution:

3.91

Write the given decimal number
without the decimal point as numerator.

In the denominator, write 1
followed by two zeros as there are 2 digits in the decimal part of the decimal
number.

= \(\frac{391}{100}\)

(ii) 2.017

Solution:

2.017

= \(\frac{2.017}{1}\)

= \(\frac{2.017 × 1000}{1 × 1000}\) ⟹
In the denominator, write 1 followed by three zeros as there are 3 digits in
the decimal part of the decimal number.

= \(\frac{2017}{1000}\)

2. Convert 0.0035 into fraction in the simplest form.

Solution:

0.0035

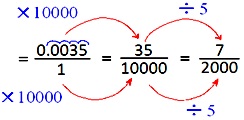
Write the given decimal number
without the decimal point as numerator.

In the denominator, write 1
followed by four zeros to the right of 1 (one) as there are 4 decimal places in
the given decimal number.

Now we will reduce the fraction
\(\frac{35}{10000}\) and obtained to its lowest term or the simplest form.

= \(\frac{7}{2000}\)

3. Express the following decimals as fractions in lowest form:

(i) 0.05

Solution:

0.05

= \(\frac{5}{100}\) ⟹ Write
the given decimal number without the decimal point as numerator.

In the denominator, write 1
followed by two zeros to the right of 1 (one) as there are 2 decimal places in
the given decimal number.

= \(\frac{5 ÷ 5}{100 ÷ 5}\) ⟹
Reduce the fraction obtained to its lowest term.

= \(\frac{1}{20}\)

(ii) 3.75

Solution:

3.75

= \(\frac{375}{100}\) ⟹ Write
the given decimal number without the decimal point as numerator.

In the denominator, write 1
followed by two zeros to the right of 1 (one) as there are 2 decimal places in
the given decimal number.

= \(\frac{375 ÷ 25}{100 ÷ 25}\) ⟹ Reduce the fraction obtained to its simplest
form.

= \(\frac{15}{4}\)

(iii) 0.004

Solution:

0.004

= \(\frac{4}{1000}\) ⟹ Write the given decimal number without the
decimal point as numerator.

In the denominator, write 1
followed by three zeros to the right of 1 (one) as there are 3 decimal places
in the given decimal number.

= \(\frac{4 ÷ 4}{1000 ÷ 4}\) ⟹ Reduce the fraction obtained to its lowest term.

= \(\frac{1}{250}\)

(iv) 5.066

Solution:

5.066

= \(\frac{5066}{1000}\) ⟹ Write the given decimal number without the decimal point as numerator.

In the denominator, write 1 followed by three zeros to the right of 1 (one) as there are 3 decimal places in the given decimal number.

= \(\frac{5066 ÷ 2}{1000 ÷ 2}\) ⟹ Reduce the fraction obtained to its simplest form.

= \(\frac{2533}{500}\)

More Examples on Converting Decimals into Fractions:

Let us consider a few more examples for converting decimals into fractions

STEPS

Step I: Remove the decimal point and write the number as the numerator of the required fraction

Step II: Write 1 as denominator.

Step III: Count the number of digits to the right of the decimal point in the decimal and write the same number of zero to the right of 1 in the denominator

4. Convert 2.7 into a fraction

Solution:

27 = \(\frac{27}{10}\)

    = 2\(\frac{7}{10}\)

Therefore, 27 = 2\(\frac{7}{10}\)

5. Convert 32.47 into a fraction.

Solution:

32.47

The denominator will have two zeros to the right of 1 because the decimal has two digits to the right of the decimal point,

32.47 = \(\frac{3247}{100}\)

         = 32\(\frac{47}{100}\)

Therefore, 32.47 = 32\(\frac{47}{100}\)

6. Convert 2.255 into a fraction

Solution:

2.255 = \(\frac{2255}{1000}\);

         =  2255/1000 

[We always reduce the fraction to its lowest terms.]

         = \(\frac{451}{200}\)

         = 2\(\frac{51}{200}\)

Thus, 2.255 = 2\(\frac{51}{200}\)

7. Convert the following decimals into a fraction

(i) 425.25

(ii) 318.4

Solution:

(i) 425.25 = \(\frac{42524}{100}\)

                = 42525/100

[We always reduce the fraction to its lowest terms.]

               = \(\frac{1701}{4}\)

               = 425\(\frac{1}{4}\)

Thus, 425.25 = 425\(\frac{1}{4}\)

(ii) 318.4 = \(\frac{3184}{10}\)

              = 3184/10

[We always reduce the fraction to its lowest terms.]

              = \(\frac{1592}{5}\)

              = 318\(\frac{2}{5}\)

Thus, 318.4 = 318\(\frac{2}{5}\)

Worksheet on Converting Decimals to Fractions:

1. Convert the given decimal numbers to fractions in the lowest
term:

(i) 1.3

(ii) 0.004

(iii) 4.005

(iv) 7.289

(v) 0.56

(vi) 21.08

(vii) 0.067

(viii) 6.66

Answers:

1. (i) \(\frac{13}{10}\)

(ii) \(\frac{1}{250}\)

(iii) \(\frac{801}{200}\)

(iv) \(\frac{7289}{1000}\)

(v) \(\frac{14}{25}\)

(vi) \(\frac{527}{25}\)

(vii) \(\frac{67}{1000}\)

(viii) \(\frac{333}{50}\)

2. Convert the following decimals into common fractions in the lowest terms:

(i) 0.7

(ii) 0.15

(iii) 0.085

(iv) 27.35

(v) 0.27

(vi) 2.08

(vii) 17.2

(viii) 5.005

(ix) 206.007

(x) 0.003

(xi) 71.035

(xii) 35.607

Answer:

2. (i) \(\frac{7}{10}\)

(ii) \(\frac{3}{20}\)

(iii) \(\frac{17}{200}\)

(iv) 27\(\frac{7}{20}\)

(v)\(\frac{27}{100}\)

(vi) 2\(\frac{2}{5}\)

(vii) 17\(\frac{1}{5}\)

(viii) 5\(\frac{1}{200}\)

(ix) 206\(\frac{7}{1000}\)

(x) \(\frac{3}{1000}\)

(xi) 71\(\frac{7}{200}\)

(xii) 35\(\frac{607}{1000}\)

3. Convert into fractions.

(i) 0.3

(ii) 23.43

(iii) 0.9

(iv) 256.58

(v) 0.7

(vi) 423.35

(vii) 0.13

(viii) 621.524

(ix) 0.24

(x) 983.45

(xi) 2.11

(xii) 898.752

(xiii) 6.27

(xiv) 252.45

(xv) 0.368

(xvi) 4.32

(xvii) 52.35

(xviii) 417.125

(xix) 7.123

(xx) 15.21

(xxi) 12.425

(xxii) 151.141

(xxiii) 131.328

(xxiv) 95.171

(xxv) 29.24

(xxvi) 14.3

(xxvii) 64.25

(xxviii) 112.32

(xxix) 46.005

(xxx) 41.55

Answer:

3. (i) \(\frac{3}{10}\)

(ii) 23\(\frac{43}{100}\)

(iii) \(\frac{9}{10}\)

(iv) 256\(\frac{29}{50}\)

(v) \(\frac{7}{10}\)

(vi) 423\(\frac{7}{20}\)

(vii) \(\frac{13}{100}\)

(viii) 621\(\frac{131}{250}\)

(ix) \(\frac{6}{25}\)

(x) 983\(\frac{9}{25}\)

(xi) 2\(\frac{11}{100}\)

(xii) 898\(\frac{94}{125}\)

(xiii) 6\(\frac{27}{100}\)

(xiv) 252\(\frac{9}{20}\)

(xv) \(\frac{46}{125}\)

(xvi) 4\(\frac{8}{25}\)

(xvii) 52\(\frac{7}{20}\)

(xviii) 417\(\frac{1}{8}\)

(xix) 7\(\frac{123}{1000}\)

(xx) 15\(\frac{21}{100}\)

(xxi) 12\(\frac{17}{40}\)

(xxii) 151\(\frac{141}{1000}\)

(xxiii) 131\(\frac{41}{125}\)

(xxiv) 95\(\frac{171}{1000}\)

(xxv) 29\(\frac{6}{25}\)

(xxvi) 14\(\frac{3}{10}\)

(xxvii) 64\(\frac{1}{4}\)

(xxviii) 112\(\frac{8}{25}\)

(xxix) 46\(\frac{1}{200}\)

(xxx) 41\(\frac{11}{20}\)

● Related Concept

● Decimals

● Decimal Numbers

● Decimal Fractions

● Like and Unlike
Decimals

● Comparing Decimals

● Decimal Places

● Conversion of
Unlike Decimals to Like Decimals

● Decimal and
Fractional Expansion

● Terminating Decimal

● Non-Terminating
Decimal

● Converting Decimals
to Fractions

● Converting
Fractions to Decimals

● H.C.F. and L.C.M.
of Decimals

● Repeating or
Recurring Decimal

● Pure Recurring
Decimal

● Mixed Recurring
Decimal

● BODMAS Rule

● BODMAS/PEMDAS Rules
– Involving Decimals

● PEMDAS Rules –
Involving Integers

● PEMDAS Rules –
Involving Decimals

● PEMDAS Rule

● BODMAS Rules –
Involving Integers

● Conversion of Pure
Recurring Decimal into Vulgar Fraction

● Conversion of Mixed
Recurring Decimals into Vulgar Fractions

● Simplification of
Decimal

● Rounding Decimals

● Rounding Decimals
to the Nearest Whole Number

● Rounding Decimals
to the Nearest Tenths

● Rounding Decimals
to the Nearest Hundredths

● Round a Decimal

● Adding Decimals

● Subtracting
Decimals

● Simplify Decimals
Involving Addition and Subtraction Decimals

● Multiplying Decimal
by a Decimal Number

● Multiplying Decimal
by a Whole Number

● Dividing Decimal by
a Whole Number

● Dividing Decimal by
a Decimal Number

7th Grade Math Problems

From Converting Decimals to Fractions to HOME PAGE