BODMAS Rule | Order of Operation |Definition,Examples,Problems

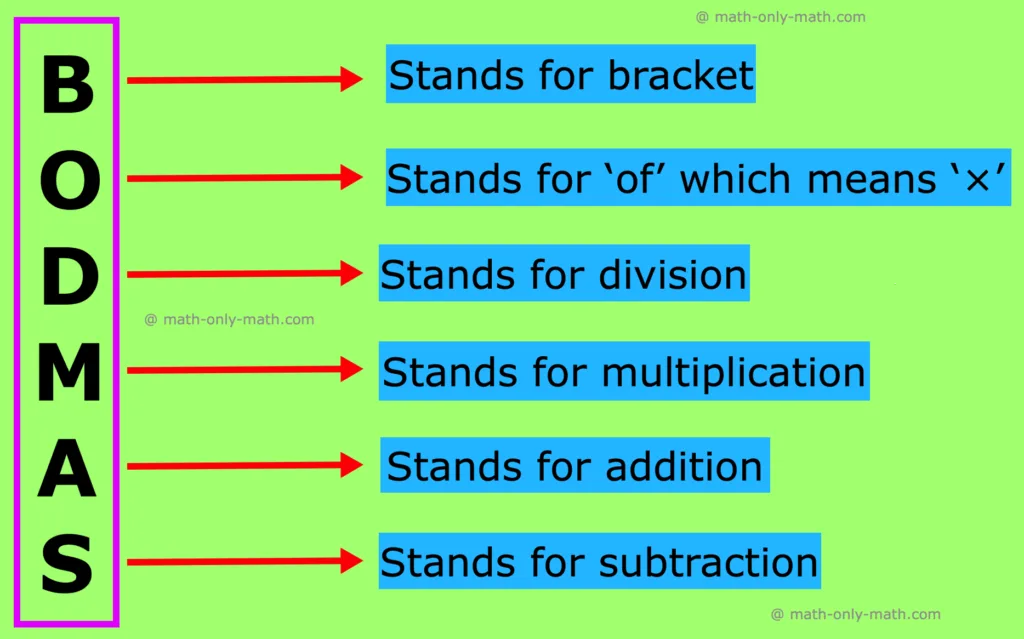
Easy and simple way to remember BODMAS rule!!

B →
Brackets
first (parentheses)

O → Of (orders i.e. Powers and Square
Roots, Cube Roots, etc.)

DM → Division
and Multiplication
(start from left to right)

AS → Addition and Subtraction
(start from left to right)

Note:

(i) Start
Divide/Multiply from left side to right side since they perform equally.

(ii) Start Add/Subtract
from left side to right side since they perform equally.

Steps to simplify the order of operation using BODMAS rule:

First part of an equation is start solving inside the ‘Brackets’.

For Example; (6 + 4) × 5

First solve inside ‘brackets’ 6 + 4 = 10, then 10 × 5 = 50.

Next solve the mathematical ‘Of’.

For
Example; 3 of 4 + 9

First solve ‘of’ 3 × 4 = 12, then 12 + 9 = 21.

Next, the part of the equation is to calculate ‘Division’ and ‘Multiplication’.

We know that, when division and multiplication follow one another, then their order in that part of the equation is solved from left side to right side.

For
Example; 15 ÷ 3
× 1 ÷ 5

‘Multiplication’ and ‘Division’ perform equally, so calculate from left to right side. First solve 15 ÷ 3 = 5, then 5 × 1 = 5, then 5 ÷ 5 = 1.

In the last part of the equation is to calculate ‘Addition’
and ‘Subtraction’. We know that, when addition and subtraction follow one
another, then their order in that part of the equation is solved from left side
to right side.

For
Example; 7
+ 19 – 11 + 13

‘Addition’ and ‘Subtraction’ perform equally, so calculate from left to right side. First solve 7 + 19 = 26, then 26 – 11 = 15 and then 15 + 13 = 28.

These are simple rules need to be followed for simplifying
or calculating using BODMAS rule.

In brief, after we perform “B“ and “O“,
start from left side to right side by solving any “D“ or “M“
as we find them. Then start from left side to right side solving any “A“
or “S“
as we find them.

MATHEMATICAL EXPRESSIONS INVOLVING DIFFERENT OPERATIONS

You have already learned about different operations such as addition, subtraction multiplication and division. Some mathematical expressions involve various operations.

For example, 9 – 12 ÷ 4 × 2 + 3

To simplify such a mathematical expression, we need to perform different operations in a certain order.

We perform the operations in the following order.

1. Division → 2. Multiplication → 3. Addition → 4. Subtraction

9 – 12 ÷ 4 × 2 + 3;  [First, do division i.e. 12 ÷ 4 = 3]

= 9 – 3 × 2 + 3;      [Now, do multiplication ie. 3 × 2 = 6]

= 9 – 6 + 3;            [Now, do addition i.e. 9 + 3 = 12]

= 9 + 3 – 6;            [As you have learned in your previous classes that the number having no sign is treated with ‘+’ sign. So, we are adding here 9 with 3 instead of 6 with 3.]

= 12 – 6                 [Finally, subtraction i.e. 12 – 6 = 6]

= 6

Note:

When we simplify a mathematical expression involving different operations, we follow the following order.

In short, we can remember DMAS where D, M, A and S are used for division, multiplication, addition and subtraction respectively.

Simplify using Four Basic Options Video

Subscribe to our YouTube channel for the latest videos, updates, and tips.

Let us consider some examples.

1. Simplify the following.

(i)  24 – 4 + 6

(ii) 20 – 15 + 7

(iii) – 9 + 20 – 3

(iv) 28 + 15 – 19

(v) 45 – 19 + 12

(vi) – 39 + 56 – 2

Solution:

These mathematical expressions involve only addition and subtraction operations. We have already learnt that if we have to addition and subtraction both together first do the addition of numbers with ‘+’ sign then do subtraction ‘-‘.

Let’s, start from addition.

(i)  24 – 4 + 6

= 24 + 5 – 4

= 29 – 4; [Addition]

= 25; [Subtraction]

Therefore, 24 – 4 + 5 = 25

(ii) 20 – 15 + 7

= 20 + 7 – 15

= 27 – 15; [Addition]

= 12; [Subtraction]

Therefore, 20 – 15 + 7 = 12

(iii) – 9 + 20 – 3

= 20 – 9 – 3

= 20 – 12

= 8; [Subtraction]

Therefore, – 9 + 20 – 3 = 8

(iv) 28 + 15 – 19

= 43 – 19; [Addition]

= 24; [Subtraction]

Therefore, 28 + 15 – 19 = 24

(v) 45 – 19 + 12

= 45 + 12 – 19

= 57 – 19; [Addition]

= 38; [Subtraction]

Therefore, 45 – 19 + 12 = 38

(vi) – 39 + 56 – 2

= 56 – 39 – 2

= 56 – 41

= 15; [Subtraction]

Therefore, – 39 + 56 – 2 = 15

2. Simplify the following.

(i) 25 – 2 × 3 + 9

(ii) 6 × 8 – 10 ÷ 5 + 4

(iii) 28 ÷ 14 × 2 + 35 – 2

(iv) 56 × 4 + 3 × 12 ÷ 4 – 7

Solution:

(i) 25 – 2 × 3 + 9

This mathematical operation is having no division. So, we start from multiplication.

25 – 2 × 3 + 9;     [Multiplication 2 × 3]

= 25 – 6 + 9;        [Now, add the numbers with ‘+’ sign]

= 25 + 9 – 6;        [Addition 25 + 9 = 34]

= 34 – 6;              [Subtraction 34 – 6 = 28]

= 28

Therefore, 25 – 2 × 3 + 9 = 28

(ii) 6 × 8 – 10 ÷ 5 + 4; [Divide 10 ÷ 5 = 2]

= 6 × 8 – 2 + 4; [Multiply 6 × 8 = 48]

= 48 + 4 – 2; [Add 48 + 4 = 52]

= 52 – 2; [Subtract 52 – 2 = 50]

= 50

Therefore, 6 × 8 – 10 ÷ 5 + 4 = 50

(iii) 28 ÷ 14 × 2 + 35 – 2; [Divide 28 ÷ 14 = 2]

= 2 × 2 + 35 – 2; [Multiply 2 × 2 = 4]

=4 + 35 – 2; [Add 4 + 35 =39]

= 39 – 2; [Subtract 39 – 2 = 37]

= 37

Therefore, 28 ÷ 14 × 2 + 35 – 2 = 37

(iv) 56 × 4 + 3 × 12 ÷ 4 – 7; [Divide 12 ÷ 4 = 3]

= 56 × 4 + 3 × 3 – 7; [Multiply 3 × 3 = 9 and 56 × 4 = 224]

= 224 + 9 – 7; [Add 224+9 = 233]

=233 – 7; [Subtract 233 – 7 = 226]

= 226

Therefore, 56 × 4 + 3 × 12 ÷ 4 – 7 = 226

MATHEMATICAL EXPRESSIONS WITH ‘BRACKETS’ AND ‘OF’

So far we have considered mathematical expressions involving operations such as addition, subtraction, multiplication and division only.

Now we will consider some different mathematical expressions with ‘brackets’ and ‘of’ also along with other operations.

Let us consider the following mathematical expression

6[425 – {66 ÷ (9 – 3)}] – 2

This expression has square brackets [ ], curly brackets { }, simple brackets ( ), and ‘of’ also apart from other mathematical operations.

While simplifying such a mathematical expression, we perform the operations in the following order.

1. We remove brackets in the following order:

    a. Simple brackets First bracket or Parenthesis or ‘( )’

    b. Curly brackets or Second bracket ‘{ }’

    c. Square brackets or Third bracket ‘[ ]’

2. ‘of’ (Remember, ‘of means multiplication)

3. Division

4. Multiplication

5. Addition

6. Subtraction

In short, we can remember BODMAS to solve such mathematical expressions Here,

Consider the above expression.

   6[425 – {66 ÷ (9 – 3)}] – 2

First we remove the brackets.

   6[425 – {66 ÷ (9 – 3)}] – 2;   First remove ( ) bracket

= 6[425 – {66 ÷ 6}] – 2;   Remove { } bracket

= 6[425 – 11] – 2; 

= 6[414] – 2;   Remove [ ] bracket

= 2484 – 2

= 2482

Therefore, 6[425 – {66 ÷ (9 – 3)}] – 2 = 2482

Note: When a number written outside of a bracket without any sign. It means we have to multiply the number with the solution of expression of that bracket.

Some mathematical expressions may have ‘^______’ also called a line bracket, above a group of numbers. In such cases, we remove this line bracket first.

We can understand the method of simplification of such mathematical expressions more clearly with the help of the following examples.

1. Simplify the following mathematical expression using BODMAS rule:

   \(\frac{5}{21}\) of [4 + {4 (15 + \(\overline{9 – 4}\))}] – 3

Solution:

  \(\frac{5}{21}\) of [4 + {4 (15 + \(\overline{9 – 4}\))}] – 3

= \(\frac{5}{21}\) of [4 + {4 (15 + 5)}] – 3; Removal of ‘^______‘

= \(\frac{5}{21}\) of [4 + {4 × 20)}] – 3; Removal of ‘( )’

= \(\frac{5}{21}\) of [4 + 80] – 3; Removal of ‘{ }’

= \(\frac{5}{21}\) of 84 – 3; Removal of ‘[ ]’

= \(\frac{5}{21}\) × 84 – 3; Removal of ‘of’

= \(\frac{5}{21}\) × \(\frac{84}{1}\) – 3; Multiplication

= \(\frac{5 × 84}{21 × 1}\) – 3

= \(\frac{420}{21}\) – 3 

= 20 – 3; Since \(\frac{420}{21}\) = 20

= 17; Subtraction.

Therefore, \(\frac{5}{21}\) of [4 + {4 (15 + \(\overline{9 – 4}\))}] – 3 = 17

2. Simplify the following mathematical expression using BODMAS rule:

\(\frac{3}{8}\) of [8 + {3 (12 – \(\overline{7 – 3}\))}] × 3

Solution:

   \(\frac{3}{8}\) of [8 + {3 (12 – \(\overline{7 – 3}\))}] × 3

= \(\frac{3}{8}\) of [8 + {3 (12 – 4)}] × 3; Removal of ‘^______‘

= \(\frac{3}{8}\) of [8 + {3 × 8}] × 3; Removal of ‘( )’

= \(\frac{3}{8}\) of [8 + 24] × 3; Removal of ‘{ }’

= \(\frac{3}{8}\) of 32 × 3; Removal of ‘[ ]’

= \(\frac{3}{8}\) × 32 × 3; Removal of ‘of’

= \(\frac{3}{8}\) × \(\frac{32}{1}\) × \(\frac{3}{1}\); Multiplication

= \(\frac{3 × 32 × 3}{8 × 1 × 1}\)

= \(\frac{288}{8}\)

= 36; Since \(\frac{288}{8}\) = 36

Therefore, \(\frac{3}{8}\) of [8 + {3 (12 – \(\overline{7 – 3}\))}] × 3 = 36

Worksheet on Simplification using BODMAS Rule

I. Simplify the following using basic four mathematical operations:

1. 54 – 3 + 4 + 9 ÷ 3

2. 62 – 24 ÷ 8 × 3 + 6

3. 28 – 2 × 5 ÷ 2 + 24 – 17

4. 48 ÷ 8 + 24 – 3 × 2

5. 64 + 8 ÷ 4 × 6 – 27

6. 55 – 3 × 6 ÷ 9 + 3

7. 14 × 5 – 72 ÷ 12 – 8 + 12

8. 25 × 5 ÷ 25 – 2 + 3

9. 17 × 4 – 27 ÷ 9 + 25

10. 8 × 8 ÷ 4 – 2 + 6

Answer:

I. 1. 58

2. 59

3. 30

4. 24

5. 59

6. 56

7. 68

8. 6

9. 90

10. 20

II. Simplify the fractions using basic four mathematical operations:

1. 102 × 4 – 7 × 4 ÷ \(\frac{2}{3}\)

2. \(\frac{2}{3}\) + \(\frac{5}{6}\) ÷ \(\frac{1}{6}\) – \(\frac{1}{9}\) × 2

3. 2\(\frac{2}{5}\) × \(\frac{4}{9}\) ÷ \(\frac{4}{7}\) + \(\frac{3}{5}\) – \(\frac{2}{5}\)

4. 2\(\frac{1}{4}\) × 8 – \(\frac{1}{8}\) × 14 + \(\frac{2}{3}\)

5. 6\(\frac{2}{3}\) + 4\(\frac{5}{12}\) ÷ \(\frac{7}{12}\) – \(\frac{5}{12}\)

6. 4\(\frac{2}{3}\) × \(\frac{2}{3}\) – \(\frac{1}{3}\) + 1\(\frac{2}{3}\) ÷ \(\frac{1}{3}\)

7. 2\(\frac{1}{4}\) × 1\(\frac{3}{5}\) + 2\(\frac{3}{4}\) ÷ \(\frac{1}{4}\) – 1\(\frac{3}{4}\)

8. 5\(\frac{1}{7}\) + 4\(\frac{1}{14}\) ÷ \(\frac{2}{7}\) × \(\frac{2}{21}\) – \(\frac{1}{7}\)

9. 4\(\frac{1}{6}\) × 2\(\frac{3}{38}\) – \(\frac{2}{7}\) + \(\frac{5}{6}\) ÷ \(\frac{1}{6}\)

10. 17\(\frac{2}{3}\) × 1\(\frac{1}{2}\) ÷ \(\frac{3}{7}\) – \(\frac{2}{7}\) + 1\(\frac{1}{3}\)

Answer:

II. 1. 366

2. 5\(\frac{4}{9}\)

3. 2\(\frac{1}{15}\) 

4. 16\(\frac{11}{12}\)

5. 13\(\frac{23}{28}\)

6. 7\(\frac{7}{9}\)

7. 12\(\frac{17}{20}\)

8. 6\(\frac{5}{14}\)

9. 3\(\frac{601}{1596}\) 

10. 62\(\frac{37}{42}\)

III. Simplify the following mathematical expressions using BODMAS rule:

1. 12 × {20 – (12 – 7)}

2. 28 × {21 + (29 – 12)}

3. 34 × (68 – (32 – 12)}

4. 96 × {30 – (18 + 10)}

5. 24 × {18 – (15 – 10)}

6. 21 × {24 + (30 – 24)}

7. 75 × {25 + (54 – 17)}

8. 54 [21 – {2 + (30 – 14)}]

9. (\(\frac{1}{3}\) – \(\frac{1}{4}\)) ÷ 1\(\frac{2}{3}\) × 4 + 2\(\frac{1}{2}\)

10. 900 ÷ (36 × 5) – 15 ÷ 3

Answer:

III. Simplify the following mathematical expressions using BODMAS rule:

1. 180

2. 1064

3. 1632

4. 192

5. 312

6. 630

7. 4650

8. 162

9. 2(\(\frac{7}{10}\)

10. 0

● Related Concept

● Decimals

● Decimal Numbers

● Decimal Fractions

● Like and Unlike
Decimals

● Comparing Decimals

● Decimal Places

● Conversion of
Unlike Decimals to Like Decimals

● Decimal and
Fractional Expansion

● Terminating Decimal

● Non-Terminating
Decimal

● Converting Decimals
to Fractions

● Converting
Fractions to Decimals

● H.C.F. and L.C.M.
of Decimals

● Repeating or
Recurring Decimal

● Pure Recurring
Decimal

● Mixed Recurring
Decimal

● BODMAS Rule

● BODMAS/PEMDAS Rules
– Involving Decimals

● PEMDAS Rules –
Involving Integers

● PEMDAS Rules –
Involving Decimals

● PEMDAS Rule

● BODMAS Rules –
Involving Integers

● Conversion of Pure
Recurring Decimal into Vulgar Fraction

● Conversion of Mixed
Recurring Decimals into Vulgar Fractions

● Simplification of
Decimal

● Rounding Decimals

● Rounding Decimals
to the Nearest Whole Number

● Rounding Decimals
to the Nearest Tenths

● Rounding Decimals
to the Nearest Hundredths

● Round a Decimal

● Adding Decimals

● Subtracting
Decimals

● Simplify Decimals
Involving Addition and Subtraction Decimals

● Multiplying Decimal
by a Decimal Number

● Multiplying Decimal
by a Whole Number

● Dividing Decimal by
a Whole Number

● Dividing Decimal by
a Decimal Number

7th Grade Math Problems

From BODMAS Rule to HOME PAGE